| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 릿코드 풀기
- 파이썬릿코드풀기
- 파이썬릿코드
- python priority queue
- 파이썬 알고리즘 풀기
- 파이썬 알고리즘
- 릿코드풀이
- 파이썬 프로그래머스
- python xor
- 파이썬알고리즘풀기
- 코틀린기초
- python Leetcode
- python 알고리즘
- leetcode풀기
- python sorted
- 릿코드 파이썬
- python zip_longest
- binary search
- leetcode 풀기
- 잇츠디모
- 릿코드
- leetcode풀이
- 릿코드풀기
- 파이썬알고리즘
- 파이썬 릿코드
- 알고리즘풀이
- LeetCode
- python 릿코드
- 알고리즘풀기
- 상가수익률계산기
- Today
- Total
소프트웨어에 대한 모든 것
[파이썬] 바이너리 서치 트리 이해 및 구현 본문
바이너리 서치 트리에(Binary Search Tree) 대해서 알아보겠습니다.
기본적인 내용은 다들 알고 계시지만 insert(), search(), delete()를 직접 구현한 분들은 많지 않을 것 같습니다. 학부 때 자료구조나 알고리즘 수업 시간에 구현을 했었을 수도 있지만 막상 당장 지금 구현하라고 하면 키보드에서 손이 멈칫 멈칫 할 것입니다.
바이너리 서치 트리(이하 BST) 구조
- 노드의 왼쪽 서브트리는 노드의 key 값 보다 작은 값을 갖는 노드로 구성
- 노드의 오른쪽 서브트리는 노드의 key 값 보다 큰 값을 갖는 노드로 구성
- 왼쪽과 오른쪽 서브트리도 각각 binary search tree로 구성되어야 함
BST 시간 복잡도
BST는 일반적으로 삽입, 탐색, 삭제는 O(logn)의 시간 복잡도를 갖습니다. BST의 worst case는 트리의 구성이
BST가 왼쪽 or 오른쪽으로 편향된 트리로 구성이 된다면 worst case에 해당이되면 O(n)의 시간 복잡도를 갖습니다.

worst case를 막고자 스스로 균형을 잡는 AVL 트리도 있습니다. AVL 이진 탐색 트리의 속성을 가지며 왼쪽/오른쪽 서브 트리의 높이 차이가 최대 1입니다. 높이 차이가 1보다 커지면 회전(rotation)을 수행해서 높이 찾이를 1로 맞춥니다. AVL 트리는 skewed 이진 트리가 만들어지지 않기 때문에 삽입, 탐색, 삭제 시간 복잡도는 O(logn)을 유지합니다. 일단 여기서는 AVL 트리가 있다는 정도만 알고가면 될 것 같습니다.

Basic Operations
- Insert - node를 tree에 추가
- Search - node를 tree에서 탐색
- Delete - 특정 node를 tree에서 삭제
- Pre-order traversal - tree를 전위순회
- In-order Traversal - tree를 중위순회
- Post-order Traversal - tree를 후위순회
Node
노드는 특정한 데이터를 갖으며 왼쪽 자식, 오른쪽 자식을 레퍼런스 할 수 있는 변수가 있어야 합니다.
class TreeNode:
def __init__(self, val):
self.val = val
self.left = None
self.right = NoneBST 클래스 정의
BinarySearchTree 클래스를 정의하고 생성자에서 root 노드를 None로 초기화합니다.
class BinarySearchTree:
def __init__(self):
self.root = NoneInsert(삽입) Operation
재귀적인 방법을 통해서 노드를 삽입 합니다. 추가하려는 값이 현재 노드의 값 보다 작을 경우는 왼쪽 자식으로 이동해서 다시 insert를 시도하고, 그렇지 않다면 오른쪽 자식으로 이동해서 insert를 시도합니다. 이동을 마지막까지 다 하고 현재 노드가 None이라면 노드를 생성하고 해당 노드를 리턴하면 이전에 재귀를 호출해던 부모 노드에 왼쪽 or 오른쪽에 달라붙게 됩니다.
def insert(self, val):
self.root = self._insert(self.root, val)
return self.root is not None
def _insert(self, node, val):
if node is None:
return TreeNode(val)
if val < node.val:
node.left = self._insert(node.left, val)
else:
node.right = self._insert(node.right, val)
return node
Search(탐색) Operation
삽입의 구현을 이해하였다면 탐색은 금방 이해가될 것입니다. 삽입처럼 재귀적으로 탐색하다가 내가 찾으려는 값과 노드의 값이 일치하면 해당 노드를 리턴하면 됩니다. 탐색 시 값의 작냐 크냐에 따라서 탐색 범위를 왼쪽 서브트리 or 오른쪽 서브트리로 범위를 줄여가기 때문에 O(logn) 시간 복잡도를 갖게 되빈다.
def search(self, val):
return self._search(self.root, val)
def _search(self, node, val):
if node is None or node.val == val:
return node
if val < node.val:
return self._search(node.left, val)
else:
return self._search(node.right, val)Delete(삭제) Operation
삭제 구현은 조금 까다롭습니다. 삭제 할 노드를 찾고, 삭제할 노드의 자식의 상태에 따라서 case가 달라집니다.
case 1 : 삭제할 노드의 왼쪽 자식이 없는 경우
case 2 : 삭제할 노드의 오른쪽 자식이 없는 경우
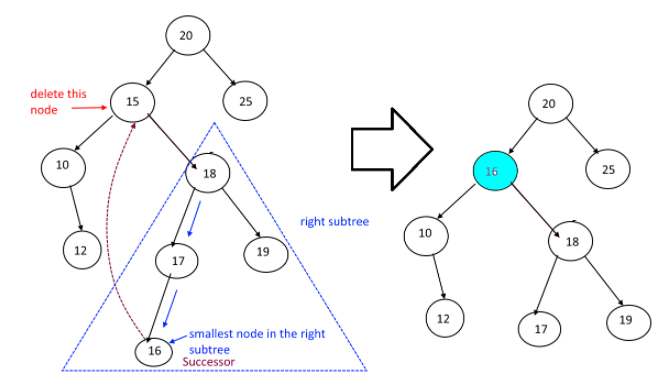
case 3 : 삭제할 노드의 왼쪽/오른쪽 자식이 있는 경우
def delete(self, val):
self.root = self._delete(self.root, val)
def _delete(self, node, val):
if node is None:
return None
if val < node.val:
node.left = self._delete(node.left, val)
elif val > node.val:
node.right = self._delete(node.right, val)
else:
if node.left is None:
return node.right
if node.right is None:
return node.left
node.val = BinarySearchTree._get_min_val(node.right)
node.right = self._delete(node.right, node.val)
return node
@classmethod
def _get_min_val(cls, node):
min_val = node.val
while node.left:
min_val = node.left.val
node = node.left
return min_val
예시 설명
순회(Traversal)
트리의 모든 노드를 방문하는 것을 순회라고 합니다.
노드를 방문하는 순서에 따라서 4가지 순회가 있습니다.
전위/중위/후위 순회는 DFS(Depth First Search)이고, 레벨 오더 순회는 (Breath First Search) 입니다.
- 전위 순회 (Preorder Traversal)
- 중위 순회 (Inorder Traversal)
- 후위 순회 (Postorder Traversal)
- 레벨 오더 순회 (LevelOrder Traversal)
전위 순회
현재 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드
def _preorder(self, node):
if node:
print(node.val, end=' ')
self._inorder(node.left)
self._inorder(node.right)
중위 순회
왼쪽 자식 노드 -> 현재 노드 -> 오른쪽 자식 노드
중위 순회로 노드를 순회하면 오름 차순 정렬된 순서로 노드를 방문하게 됩니다.
def _inorder(self, node):
if node:
self._inorder(node.left)
print(node.val, end=' ')
self._inorder(node.right)
후위 순회
왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 현재 노드
def _postorder(self, node):
if node:
self._inorder(node.left)
self._inorder(node.right)
print(node.val, end=' ')레벨 오더 순회
덱 자료구조를 사용해서 레벨 오더 순회를 구현합니다.
이전 글을 참고하시면 이해가 더 쉽습니다.
2021.11.20 - [알고리즘/알고리즘 Basic] - 이진 트리 레벨 순회 (Binary Tree Level Order Traversal)
이진 트리 레벨 순회 (Binary Tree Level Order Traversal)
이진 트리 레벨 순회는 이진 트리의 낮은 레벨의 노드부터 순차적으로 방문합니다. 트리를 너비우선탐색(BFS(Breadth first search)) 하는 것 입니다. 위 그림에서, Level1 - 1 Level2 - 2, 3 Level3 - 4, 5, 6,..
wellsw.tistory.com
def level_order(self, node):
if node is None:
return
queue = deque()
queue.append(node)
level = 0
while queue:
values = []
for _ in range(len(queue)):
cur = queue.popleft()
if cur:
values.append(cur.val)
queue.append(cur.left)
queue.append(cur.right)
if values:
print(f'level : {level}, values : {values}')
level += 1
전체 소스 코드
from collections import deque
class TreeNode:
def __init__(self, val):
self.val = val
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, val):
self.root = self._insert(self.root, val)
return self.root is not None
def _insert(self, node, val):
if node is None:
return TreeNode(val)
if val < node.val:
node.left = self._insert(node.left, val)
else:
node.right = self._insert(node.right, val)
return node
def search(self, val):
return self._search(self.root, val)
def _search(self, node, val):
if node is None or node.val == val:
return node
if val < node.val:
return self._search(node.left, val)
else:
return self._search(node.right, val)
def delete(self, val):
self.root = self._delete(self.root, val)
def _delete(self, node, val):
if node is None:
return None
if val < node.val:
node.left = self._delete(node.left, val)
elif val > node.val:
node.right = self._delete(node.right, val)
else:
if node.left is None:
return node.right
if node.right is None:
return node.left
node.val = BinarySearchTree._get_min_val(node.right)
node.right = self._delete(node.right, node.val)
return node
@classmethod
def _get_min_val(cls, node):
min_val = node.val
while node.left:
min_val = node.left.val
node = node.left
return min_val
def to_list(self):
return self._to_list(self.root)
def _to_list(self, node):
if node is None:
return []
return self._to_list(node.left) + [node.val] + self._to_list(node.right)
def print_by_ascending(self):
self._inorder(self.root)
def _preorder(self, node):
if node:
print(node.val, end=' ')
self._inorder(node.left)
self._inorder(node.right)
def _inorder(self, node):
if node:
self._inorder(node.left)
print(node.val, end=' ')
self._inorder(node.right)
def _postorder(self, node):
if node:
self._inorder(node.left)
self._inorder(node.right)
print(node.val, end=' ')
def level_order(self, node):
if node is None:
return
queue = deque()
queue.append(node)
level = 0
while queue:
values = []
for _ in range(len(queue)):
cur = queue.popleft()
if cur:
values.append(cur.val)
queue.append(cur.left)
queue.append(cur.right)
if values:
print(f'level : {level}, values : {values}')
level += 1
nums = [10, 3, 4, 11, 32, 21, 45, 8, 1, 18]
bst = BinarySearchTree()
for n in nums:
bst.insert(n)
print('\n\n오름 차순 정렬 출력')
bst.print_by_ascending()
# Search
assert bst.search(10) is not None
assert bst.search(18) is not None
assert bst.search(100) is None
# Delete
bst.delete(10)
bst.delete(18)
assert bst.search(10) is None
assert bst.search(18) is None
print('\n\n오름 차순 정렬 출력')
bst.print_by_ascending()
print('\n\n레벨 오더 순회')
print(bst.level_order(bst.root))
print('\n\n이진 트리의 값을 오름 차순 정렬 리스트 자료구조로 반환')
print(bst.to_list())
함께 보면 좋을 글:
https://www.geeksforgeeks.org/binary-search-tree-data-structure/
https://www.gatevidyalay.com/binary-search-trees-data-structures/
'알고리즘 > 알고리즘 Basic' 카테고리의 다른 글
| [파이썬] Floyd's Cycle Detection 알고리즘 (0) | 2022.03.03 |
|---|---|
| [파이썬] 배열을 바이너리 서치 트리로 변환 ( array to height balanced Binary Search Tree) (0) | 2022.02.27 |
| [파이썬] 덱 vs 리스트 속도 차이? (deque vs list speed 차이) (1) | 2021.11.29 |
| 이진 트리 레벨 순회 (Binary Tree Level Order Traversal) (0) | 2021.11.20 |
| [파이썬] 바이너리 서치 (이진 탐색) (0) | 2021.11.10 |