Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- binary search
- 파이썬 알고리즘
- python xor
- 릿코드 파이썬
- 파이썬 프로그래머스
- 알고리즘풀기
- 파이썬릿코드풀기
- python sorted
- leetcode풀기
- 릿코드 풀기
- python Leetcode
- 릿코드풀기
- 파이썬릿코드
- leetcode풀이
- python zip_longest
- 릿코드풀이
- 파이썬알고리즘
- 알고리즘풀이
- leetcode 풀기
- python 알고리즘
- python priority queue
- LeetCode
- 코틀린기초
- 릿코드
- 파이썬 릿코드
- 상가수익률계산기
- 잇츠디모
- 파이썬알고리즘풀기
- 파이썬 알고리즘 풀기
- python 릿코드
Archives
- Today
- Total
소프트웨어에 대한 모든 것
931. Minimum Falling Path Sum 본문
반응형
문제)
Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.
A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).
Example 1:
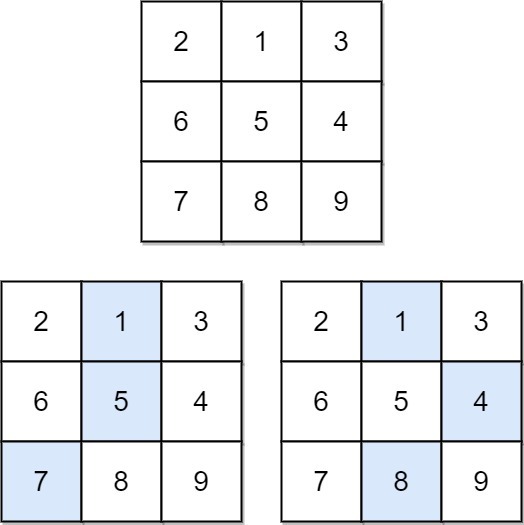
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]]
Output: 13
Explanation: There are two falling paths with a minimum sum as shown.
Example 2:
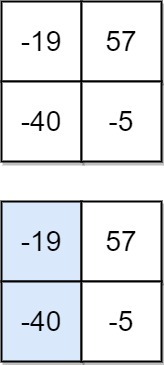
Input: matrix = [[-19,57],[-40,-5]]
Output: -59
Explanation: The falling path with a minimum sum is shown.
Constraints:
- n == matrix.length == matrix[i].length
- 1 <= n <= 100
- -100 <= matrix[i][j] <= 100
문제 이해)
- 0 row에서 부터 시작해서 element를 선택해서 다음 row로 이동새 col은 col-1, col, col+1을 선택할 있다. 최종 row까지 도달 시 mimum sum은 무엇인가?
- 문제를 단순화하면 0번째 row에서 n-1번째까지 이동하는데 가장 짧은 거리는?
- 테이블을 하나 생성해서 현재 기준으로 가장 최소 path를 저장해간다면 O(n)에 문제 풀이가 가능
솔루션1)
class Solution:
def minFallingPathSum(self, matrix):
n = len(matrix)
dp = [[0] * n for i in range(n)]
for r in range(n):
for c in range(n):
if r == 0:
dp[r][c] = matrix[r][c]
elif c == 0:
# first column
dp[r][c] = matrix[r][c] + min(dp[r-1][c], dp[r-1][c+1])
elif c == (n-1):
# last column
dp[r][c] = matrix[r][c] + min(dp[r-1][c-1], dp[r-1][c])
else:
dp[r][c] = matrix[r][c] + min(dp[r - 1][c - 1], dp[r - 1][c], dp[r - 1][c+1])
return min(dp[-1])솔루션2)
솔루션1에서 dp 테이블을 만들지 않고 더 간결화한 코드
class Solution:
def minFallingPathSum(self, matrix):
n = len(matrix)
for r in range(1, n):
for c in range(n):
if c == 0:
# first column
matrix[r][c] = matrix[r][c] + min(matrix[r-1][c], matrix[r-1][c+1])
elif c == (n-1):
# last column
matrix[r][c] = matrix[r][c] + min(matrix[r-1][c-1], matrix[r-1][c])
else:
matrix[r][c] = matrix[r][c] + min(matrix[r - 1][c - 1], matrix[r - 1][c], matrix[r - 1][c+1])
return min(matrix[-1])
반응형
'알고리즘 > LeetCode' 카테고리의 다른 글
| 451. Sort Characters By Frequency (0) | 2022.12.14 |
|---|---|
| 1704. Determine if String Halves Are Alike (0) | 2022.12.14 |
| 2432. The Employee That Worked on the Longest Task (0) | 2022.12.09 |
| 1026. Maximum Difference Between Node and Ancestor (0) | 2022.12.09 |
| 6. Zigzag Conversion (0) | 2022.12.07 |
Comments