Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- 알고리즘풀기
- 파이썬알고리즘풀기
- binary search
- 파이썬알고리즘
- python zip_longest
- python 알고리즘
- 파이썬릿코드
- leetcode 풀기
- 잇츠디모
- 코틀린기초
- 파이썬 알고리즘 풀기
- 릿코드 파이썬
- LeetCode
- python 릿코드
- python sorted
- leetcode풀이
- 파이썬 알고리즘
- python priority queue
- 파이썬릿코드풀기
- leetcode풀기
- 상가수익률계산기
- 릿코드 풀기
- python Leetcode
- 릿코드풀기
- 릿코드풀이
- 파이썬 릿코드
- 릿코드
- 알고리즘풀이
- python xor
- 파이썬 프로그래머스
Archives
- Today
- Total
소프트웨어에 대한 모든 것
LeetCode 풀기 - 64. Minimum Path Sum 본문
반응형
64. Minimum Path Sum
https://leetcode.com/problems/minimum-path-sum/
Minimum Path Sum - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
문제)
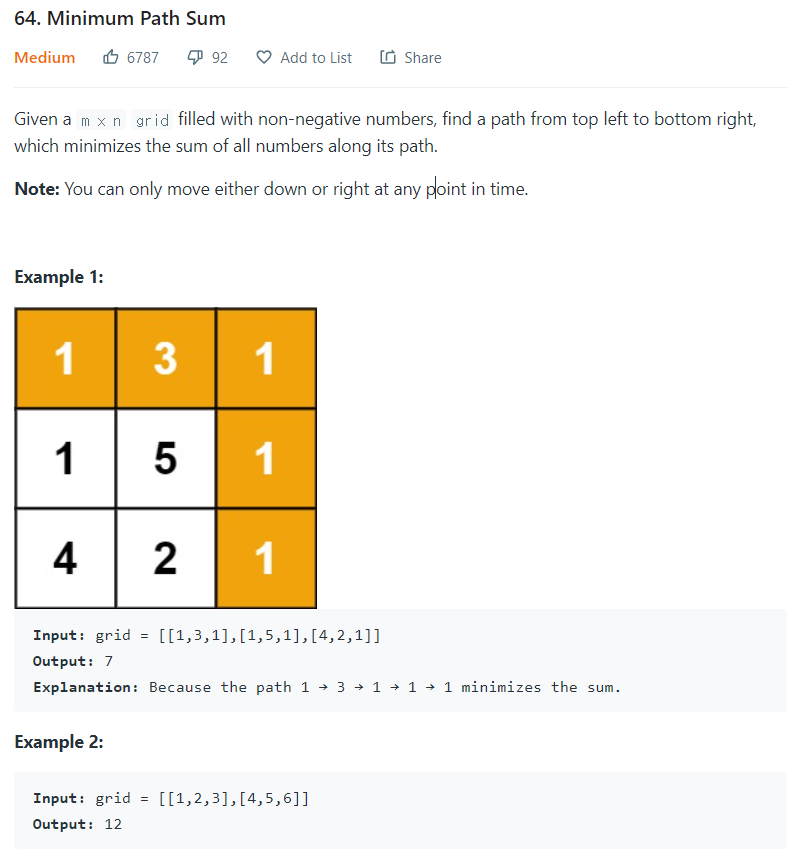

솔루션1) iterative
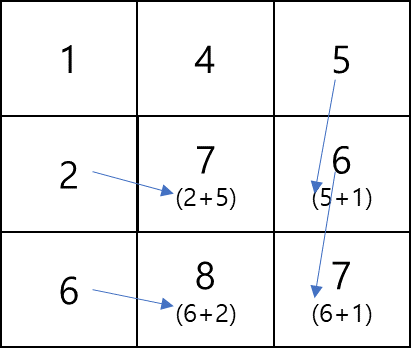
Bottom-up 방식으로 풀어 나갑니다.
먼저 0행을 초기화합니다.

0열을 초기화합니다.

이제 m-1행, n-1을 향해서 순차적으로 채워나갑니다.
채워 나갈 때 최소 sum을 구하면서 채워 나갑니다.
예를 들어 grid[1][1]은 grid[1][0]과 grid[0][1]에서 최소값인 2를 선택해서 자기 자신 5와 더해서 7이 됩니다.
이를 끝까지 반복해 나갑니다.
class Solution:
def minPathSum(self, grid):
# iterative
m, n = len(grid), len(grid[0])
# 첫번째 행 초기화
for col in range(1, n):
grid[0][col] = grid[0][col - 1] + grid[0][col]
# 첫번째 열 초기화
for row in range(1, m):
grid[row][0] = grid[row - 1][0] + grid[row][0]
# bottom-up
for row in range(1, m):
for col in range(1, n):
grid[row][col] += min(grid[row][col-1], grid[row-1][col])
return grid[m-1][n-1]솔루션2) iterative 개선
import math
class Solution:
def minPathSum(self, grid):
m, n = len(grid), len(grid[0])
memo = [[0] * n for i in range(m)]
memo[0][0] = grid[0][0]
for r in range(m):
for c in range(n):
if r == 0 and c == 0:
continue
left = memo[r][c-1] if c > 0 else math.inf
up = memo[r-1][c] if r > 0 else math.inf
memo[r][c] = min(left, up) + grid[r][c]
return memo[m-1][n-1]
솔루션3) Dynamic Programming
동적 계획법을 이용해서 풉니다.
점화식은 아래와 같은 형식입니다.
f(row, col) = min(f(row-1, col), f(row, col-1) + grid[row][col]
memo 변수를 하나 추가해서 이전에 계산 했던 기록을 저장합니다.
class Solution:
def minPathSum(self, grid):
# Dynamic Programming
m, n = len(grid), len(grid[0])
memo = [[-1]*n for i in range(m)]
memo[0][0] = grid[0][0]
for col in range(1, n):
memo[0][col] = memo[0][col-1] + grid[0][col]
for row in range(1, m):
memo[row][0] = memo[row - 1][0] + grid[row][0]
def dp(row, col):
if memo[row][col] != -1:
return memo[row][col]
memo[row][col] = min(dp(row-1, col), dp(row, col-1)) + grid [row][col]
return memo[row][col]
return dp(m-1, n-1)
반응형
'알고리즘 > LeetCode' 카테고리의 다른 글
| LeetCode 풀기 - 287. Find the Duplicate Number (0) | 2022.03.02 |
|---|---|
| LeetCode 풀기 - 34. Find First and Last Position of Element in Sorted Array (0) | 2022.02.28 |
| LeetCode 풀기 - 108. Convert Sorted Array to Binary Search Tree (0) | 2022.02.27 |
| LeetCode 풀기 - 662. Maximum Width of Binary Tree (0) | 2022.02.27 |
| LeetCode 풀기 - 49. Group Anagrams (0) | 2022.02.26 |
Comments




